The Options Encyclopedia

By Kanu Gupta and Eshan Gupta

Learning to invest through basic stocks can be a daunting task as it takes immense effort and dedication to master. Investing is seen as a reasonable method to grow wealth over time; the process begins with a small amount of  money and results in it growing exponentially through compound interest over time. Despite investing seeming to be the best method to grow wealth for those who are not already prosperous, the practice of investing in the stock market attracts far more interest from those who are already wealthy. This is because the rich can afford to either put in the work to make solid investing decisions or hire financial advisors to manage their capital for them, while those in lower financial classes either do not have the resources to employ professionals or do not have enough capital to make investing worthwhile.

A solution to make the stock market more appealing to those with less money was devised: leverage. Consider this: your grandma gifted you $100 for your birthday. But you want to buy 10 shares of Apple ($130 * 10 = $1300). Obviously, you don’t have the money for that, so you will go to your parents and ask them to loan you $1200 (so you have enough money to invest now). You invest the $1300 and the next day (hypothetically) Apple announces that they are releasing the Apple Car! The stock shoots up 10% and your $1300 investment becomes $1430! You return $1230 to your parents (their original $1200 and $30 interest, or a fee to borrow money) and you’re left with $200 instead of $110 (which is the amount you’d be worth if you just invested $100). Leverage, a form of debt, is the use of funds that do not belong to the buyer of the asset. One form that leverage comes in is margin, which is borrowing money from your broker (not your parent) in order to make purchases that you are not able to afford. However, another form of leverage (what this article is about) is option contracts. Due to their volatility, options are popular amongst those who either prefer to gamble or do not have enough capital to make 8% yearly returns worthwhile (making $8 off of an initial investment of $100 a year isn’t really worthwhile). 

Before we proceed, please read this disclaimer:

It is absolutely crucial to note that options are not an excuse to ignore investing principles and avoid learning how to invest properly. The sole purpose of this article is to provide an introductory guide to what options are, how they work, and how to make money with them. As you will learn ahead, options come with potentially unlimited risk and you can lose much more than your initial investment, so proceed with absolute caution. 

What is an option?

An options contract is a contract, or agreement, between the buyer of the option and the seller of the option. The buyer gains the right (not obligation or requirement) to either buy or sell shares of a company (known as exercising the option) at an agreed-upon price (which is known as the strike price) by an agreed-upon date  (known as the date of expiry in the U.S.). After the option has expired, it becomes worthless and can no longer be exercised.

As an example, here is a call option (explained ahead) contract for Boeing ($BA) with an expiry date of March 25, 2022, and a strike price of $192.5.

Important Note: Options only come in packages of 100, so each option contract represents 100 individual options. For example, one option contract on $BA is automatically translated to 100 individual options, resulting in a $242 purchase of 100 separate $2.42 option contracts. Note that the order above is only for one option contract, but the broker automatically translates it to 100 options, shown by the (+1 BA 100).

The two types of options:

The two types of options are call and put options. Call options grant the buyer the right to buy a share of stock at a strike price, while a put option grants the buyer the right to sell a share of stock at a strike price. Call options and put options are often referred to as calls and puts for the purpose of simplicity. The relationship between a call and a put is similar to that of a stock and a short. A call option makes money when the stock goes up, while a put option makes money when the stock goes down. Check out this graphic to get a clear understanding: 

The cost of an option and the factors that determine it:

Without a cost, an option would be a source of infinite money. One could buy a call options contract with a low strike price and exercise it, immediately making a profit equal to their strike price subtracted from the stock price. To avoid this, an option contract comes with a cost known as the premium. The premium is calculated by adding the two different values of an option, intrinsic and extrinsic, to each other. 

The intrinsic value for a call option is the strike price subtracted from the current stock price, while a put option’s intrinsic value is equal to the stock price subtracted from the strike price. This is because a call option makes money when the stock price goes up, so the stock price already being above the strike price increases the value of the option. Conversely, a put option makes money when the stock price goes down, so the stock price being below the strike price gives the option additional value. A more intuitive definition for intrinsic value is the amount of money made by exercising the option.

Math behind intrinsic value

The equation for intrinsic value is IV = S - K for call options and IV = K - S for put options, where S = stock price and K = strike price. For example, a $100 (K) strike call option for a $110 (S) stock would have an intrinsic value of $10 (using IV = S - K for calls). However, a $100 strike put option for a $110 stock would have an intrinsic value of $0 (using IV = K - S for puts), since $100 - $110 is a negative number and the minimum intrinsic value is 0.

The intrinsic value has opposite definitions for a call option and a put option, so it has been summarized into one equation for the purposes of simplicity.

Extrinsic Value

The extrinsic value is known as the “time value” of the option and is far more complex than the intrinsic value. It is the worth that is assigned to an options contract by factors other than the underlying asset price. The extrinsic value is calculated using the volatility of the stock (known as implied volatility), the amount of time until the option’s expiry, and the movement of the stock price. Naturally, if the extrinsic value is priced based on the amount of time until the option’s expiry, it will decay as the time to expiry decreases. This process, known as time decay, results in the extrinsic value depleting all the way to 0 on the date of expiry, leaving only the intrinsic value to determine the value of the option. For example, an option with a $10 intrinsic value and a $15 extrinsic value, would have an initial premium of $25. By the day of expiry, the extrinsic value will decay to $0, resulting in a $10 value since the $10 intrinsic value is the only factor determining the value of the option.

Implied Volatility

Before moving on to how extrinsic value is mathematically calculated, it is important to understand the fundamentals of its properties. Time to expiry and the movement of the stock price are understandable, but what is implied volatility?

The implied volatility (IV) of an option is a quantified metric that gauges the likelihood that the option changes in price. Essentially, it’s a measure of how much a stock is moving up and down. Implied Volatility is quantified as a percentage. If the underlying stock becomes more unpredictable and risky, the implied volatility will increase since it becomes more likely that the option will move heavily in price in the near future. Some examples of situations that would cause a high IV are upcoming earnings or a Black Swan event triggering increased options trading activity.

The math behind extrinsic value

How exactly do changes in IV, time to expiry, and the stock price affect the extrinsic value of the option? How are these variations calculated? The math behind it is represented by the Black-Scholes model, a Nobel Prize winning formula created by Fischer Black, Myron Scholes, and Robert Merton, economists and graduates of the Massachusetts Institute of Technology (aka MIT). 

The complexity of the formula raises an important question. How do investors simplify and categorize the effects of the Black-Scholes formula into something more easily understood?

The Greeks

The answer to this question is the Greek variables: Delta Δ, Gamma γ, Theta θ, and Vega ν. All of these Greek variables are referred to as their corresponding Greek letter except for Vega, whose symbol is the Greek letter Nu. Each Greek corresponds to one aspect of Extrinsic Value. Delta and Gamma both correspond to the stock price, Theta corresponds to time value, and Vega to Implied Volatility. All Greek variables are quantified in a $ amount, not a %, so they are quite straightforward. Note, there’s a calculus and complex math warning for the topics below. 

Delta and Gamma

Delta is the $ amount that the extrinsic value for a call option will increase for each $1.00 increase in the stock price. For example, a $5.00 call option with a Delta of $0.50 would increase by that Delta if the stock price increased by $1.00 to a new $5.50. Conversely, a $5.00 put option with the same Delta would decrease by $0.50 if the stock price increased by $1.00, since put options make money when the stock decreases. The Delta will usually maximize at $1.00. In this situation, the extrinsic value would increase by $1 for each $1 increase in the stock price, essentially acting like the stock itself.

Gamma is the $ amount that the Delta for a call option will increase for each $1.00 increase in the stock price. Let’s say that the above example with a $5.00 call option with a Delta of $0.50 has a Gamma of $0.05. If the stock price increased by $1.00, the extrinsic value would increase to $5.50, and the Delta would increase by the Gamma to $0.55. If the stock price increased by another $1.00, the extrinsic value would increase by the Delta to $6.05, and the Delta would increase by the Gamma to $0.60. The opposite effect occurs for a put option. A $5.00 put option with a Delta of $0.50 and a gamma of $0.05 would result in the extrinsic value decreasing to $4.50 and the Delta decreasing to $0.45 for the first $1.00 increase in the stock price and the extrinsic value decreasing to $4.05 and the Delta decreasing to $0.40 for the second $1.00 increase in the stock price. The one issue with this example is that Gamma also changes when the stock price changes, but that issue will be tackled after the basics of Gamma and Delta have been fully explained. 

There are a few analogies that help explain the relationship between Delta and Gamma. The physics analogy is limited since it fails to explain the change in Gamma and the general shapes of the Delta and Gamma graphs, but it is here regardless as a resource. The mathematics analogy is much more comprehensive and can explain the shapes of the Delta and Gamma graphs as a function of stock price.

Real Life

Think of the option’s extrinsic value as a car on a straight road. The Delta is the velocity of the car, so if the stock price stays constant, the car will remain at rest. In regular physics, velocity is equal to (displacement of the car)/(amount of time the car has traveled). Plugging in our analogy in which the car represents the extrinsic value and time represents the stock price, Delta in option “physics” is equal to ($ change in Extrinsic Value)/($ change in stock price). This equation, Δ = (Change in EV/change in Stock Price), can be rewritten as Δ * change in Stock Price = change in Extrinsic Value. This equation is quite similar to the physics equation velocity * time = displacement. 

Gamma is the acceleration of the car, so if the stock price stays constant, the car will not accelerate. In typical physics, acceleration = (change in velocity)/(change in time). Once again plugging in for the analogy, Gamma = ($ change in Delta)/($ change in stock price), which can be rewritten as γ * change in Stock Price = change in Delta. This equation is similar to the kinematics equation acceleration * time = change in velocity. However, this equation can only be used for a $1.00 change in stock price because Gamma, or acceleration in this analogy, changes as the stock price changes.

Mathematics

The extrinsic value of the option can be seen as a function of stock price, S, represented as a function f(S). The x-axis is the stock price and the y-axis is the extrinsic value of the option. The Delta is the first derivative of this function, or d(EV)/dS. Gamma is the second derivative of the function, or d^2(EV)/dS^2. 

Because of Gamma, it is given that Delta will change as the stock price increases for call options. It was stated earlier that Gamma also changes, but what variable determines this change? Unfortunately, there is no mathematical variable that determines what the change in Gamma will be. However, the properties of how Gamma changes are known. Gamma is maximized at the strike price, and slowly curves out as the stock price diverges from the strike price. The formed shape looks like a hill or a wave crest. Using the wave crest analogy, the Implied Volatility is related to the amplitude of the wave. A lower implied volatility will result in a higher amplitude, or more variation between the Gammas for different stock prices.

Given the above graph of possible Gammas for different Implied Volatilities, what is the strike price of the option that the Gamma pertains to? The answer is $25, since Gamma maximizes at the strike price of the option and curves out as the stock price moves away from the strike price. 

Here is a visual that shows the general shape of both Delta and Gamma for the same strike price of $25 for a call option. An unidentified Implied Volatility is used here. The Delta graph can be approximated as a Sigmoid function, forming horizontal asymptotes at Delta = $0 and Delta = $1.

(Pictured above is a Desmos graph of both a sigmoid function and the derivative of the sigmoid function). Note the similarity between the Desmos graph and the Gamma & Delta graph.

An “optional” delve into the ways Delta and Gamma affect an option:

Since Gamma is always positive, Delta is always increasing, which means that as the stock price decreases, Delta decreases. If the stock price is significantly less than the strike price, the option’s extrinsic value will be nearly $0 and will have a Delta and Gamma close to $0. The option would also be OTM and have an intrinsic value of $0. This makes the option very undesirable and low-quality. The portion of the extrinsic value of an option that Delta and Gamma contribute to can be calculated using the integral from 0 to the current stock price for Delta. This means that the area under the curve of Delta is equal to the contribution of Delta and Gamma to the stock price of the option. Essentially, if both Delta and Gamma are very close to $0 like they are when the stock price is much lower than the strike price for a call option, they will have contributed no value to the extrinsic value of the option. This would make the option both extremely cheap and extremely unlikely to make money given that both Delta and Gamma are $0. Conversely, if the stock price is significantly higher than the strike price, both Delta and the extrinsic value will be extremely high, but the Gamma will have leveled off to approximately 0. This new option is much higher-quality and ITM, and the properties of Delta and Gamma will result in this option being much more expensive than the previous example. Note that many of the effects listed here pertain to call options and are the opposite for put options.

Key Example: Increasing the intensity of this example, a call option at a stock price vastly higher than its strike price would have a maximized Delta of $1, a minimized Gamma of $0, and a total option value very close to the price of the stock itself (using intrinsic value along with the Delta of $1 increasing the option’s value). In this scenario, the option is basically the stock itself, and it would be essentially the same as exercising the option or just simply buying the stock itself and skipping the whole option process.

Theta

Theta is perhaps the most disliked Greek out of the four by most options traders; it represents the $ amount that the extrinsic value declines for each day until the option’s expiry. 

A graph of the extrinsic value of an option and theta’s effect on it over time.

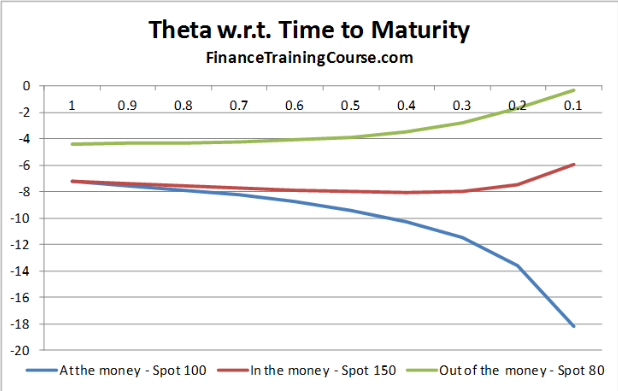
A graph of theta itself for ATM, ITM, and OTM options.

Theta is non-linear and its effect on the extrinsic value of an option can generally be approximated as exponential decay. The general shape of the theta graph is similar for all types of options since it is a function of time, which is a completely independent variable. Time decay is an important factor to consider when trading options, because the potential profit could be completely counteracted by time decay in options close to expiry. Theta for both ITM and OTM options tends to spike in the days approaching expiry, yet sharply decreases for ATM options. The likelihood that an option will be exactly at the money before expiry is fairly low, however, so one should always prepare for an increase in decay as the option approaches expiry. Options with a higher time to expiry have a larger protective cushion against theta, making them more desirable and thus more expensive.

An example of Theta at work is a $5.00 option with a theta of $-0.20 on a Thursday. After one day, given that the stock price and implied volatility remain constant, the option’s new value would be $5.00 - $0.20 = $4.80. Theta does still cause decay over weekends, so there would be three days of decay from Friday to Monday, or $0.60. The option’s value on Monday would be $4.80 - 3($0.20) = $4.20.

Vega

The final Greek variable is Vega, which is the $ increase in extrinsic value for each % increase in Implied Volatility. The definition of Implied Volatility is the forecasted volatility of the stock that the option pertains to. Events that could lead to an increase in IV are a bear market, upcoming earnings, and unexpected news or developments related to the stock. For example, approaching earnings for GME could cause the Implied Volatility to increase from 30% to 80%. For a GME option with a Vega of $0.05, the increase in extrinsic value as a result of Vega would be $0.05 * (80 - 30) = $2.50. 

IV and IV Crush

Since Implied Volatility sharply increases before a company’s earnings or right after a big announcement, it is only natural for the IV to drop off just after earnings or as time progresses from the important announcement, causing the option’s value to sharply decline as a result of Vega. This process is known as IV crush, which gets its name due to the decline in Implied Volatility “crushing” the value of the option. 

Unfortunately, many beginner options traders fall victim to IV crush, since the heightened volatility entices them into making purchases in the hopes of the massive gains often seen on r/Wallstreetbets. However, r/WSB is not a realistic representation of how options behave, since buying options in times of high volatility is usually risky due to the impending decline in IV. Options traders should always pay attention to the Implied Volatility of their options and be aware of any possibility of IV crush occurring. 

An observational side note

Due to high-quality and profit making options being more expensive, it is an undeniable fact that it is safer and easier to make money with options with a larger amount of capital. The factors that make an option more likely to make money also makes it much more expensive, such as a high Gamma and Delta, a lengthy amount of time to the expiry date, and a safe cushion of intrinsic value to prevent the option from becoming worthless. This contributes to the phenomenon of small options traders regularly placing risky bets and losing all of their capital on low-quality and cheap options. This strikes a parallel to the regular stock market because small traders usually prefer to trade low-cost and risky penny stocks instead of more expensive blue-chip and fundamentally sound businesses. This is a quick crash course of this complex financial instrument, so exercise caution!